Matrix Core Programming on AMD CDNA™3 and CDNA™4 architecture

Matrix Core Programming on AMD CDNA™3 and CDNA™4 architecture#

September 30, 2025 by Amanzhol Salykov, Andy Luo, Carlus Huang, Peng Sun.

15 min read. | 3655 total words.

AI/ML, C++, Linear Algebra, HPC, Performance, Optimization, Hardware

Developers, HPC, AI, Systems

In this blog post, we walk through how to use Matrix Cores in HIP kernels, with a focus on low-precision data types such as FP16, FP8, and FP4, as well as the new family of Matrix Core instructions with exponent block scaling introduced in the AMD CDNA™4 architecture. Through code examples and illustrations, we provide the necessary knowledge to start programming Matrix Cores, covering modern low-precision floating-point types, the Matrix Core compiler intrinsics, and the data layouts required by the Matrix Core instructions.

Matrix Cores#

Matrix multiplication is an essential part of AI and HPC workloads. The AMD CDNA™ architecture features special-purpose hardware, the Matrix Cores, to accelerate matrix fused-multiply-add (MFMA) operations defined as D:=A*B+C. Please note that MFMA instructions are often used to update a matrix in-place (=accumulation) so that D=C and C:=A*B+C. The matrices A and B are called input matrices, while the matrix D is referred to as the output matrix or accumulator.

The performance gains from using Matrix Cores are especially significant in mixed-precision mode, where the input matrices use lower-precision data types instead of FP32. The output matrix, however, is stored in FP32 to minimize accuracy loss during accumulation. The tables below show the theoretical peak performance of Matrix Cores with different input data types on both AMD CDNA™3 and AMD CDNA™4 architectures. On the AMD Instinct™ MI325X, using FP16 input matrices delivers nearly an 8x performance increase compared to single-precision, with only minimal accuracy loss. Switching to FP8 further doubles the performance providing a 16x increase when compared to FP32. The AMD CDNA™4 architecture further improves Matrix Core performance, delivering up to 2x higher throughput for FP16 and FP8 compared to the AMD CDNA™3 architecture. In addition, AMD CDNA™4 introduces new low-precision data types such as FP6 and FP4, enabling up to 64x performance gain relative to FP32. Please refer to the AMD CDNA™3 and AMD CDNA™4 white papers for detailed architecture specifications.

Type	AMD Instinct™ MI325X (CDNA™3)	Speedup vs. FP32
Matrix FP64	163.4 TF	1x
Matrix FP32	163.4 TF	1x
Matrix FP16	1307.4 TF	~8x
Matrix FP8	2614.9 TF	~16x

Type	AMD Instinct™ MI355X (CDNA™4)	Speedup vs. FP32
Matrix FP64	78.6 TF	~0.5x
Matrix FP32	157.3 TF	1x
Matrix FP16	2.5 PF	~16x
Matrix FP8	5 PF	~32x
Matrix FP6	10 PF	~64x
Matrix FP4	10 PF	~64x

Low-Precision Floating-Point Types#

A binary representation of a floating-point number consists of n bits, where m of n bits represent the mantissa, 1 bit determines the sign and n-m-1 bits represent the exponent. The following image illustrates the binary format of a floating-point number and how the exponent and mantissa are calculated based on its binary representation.

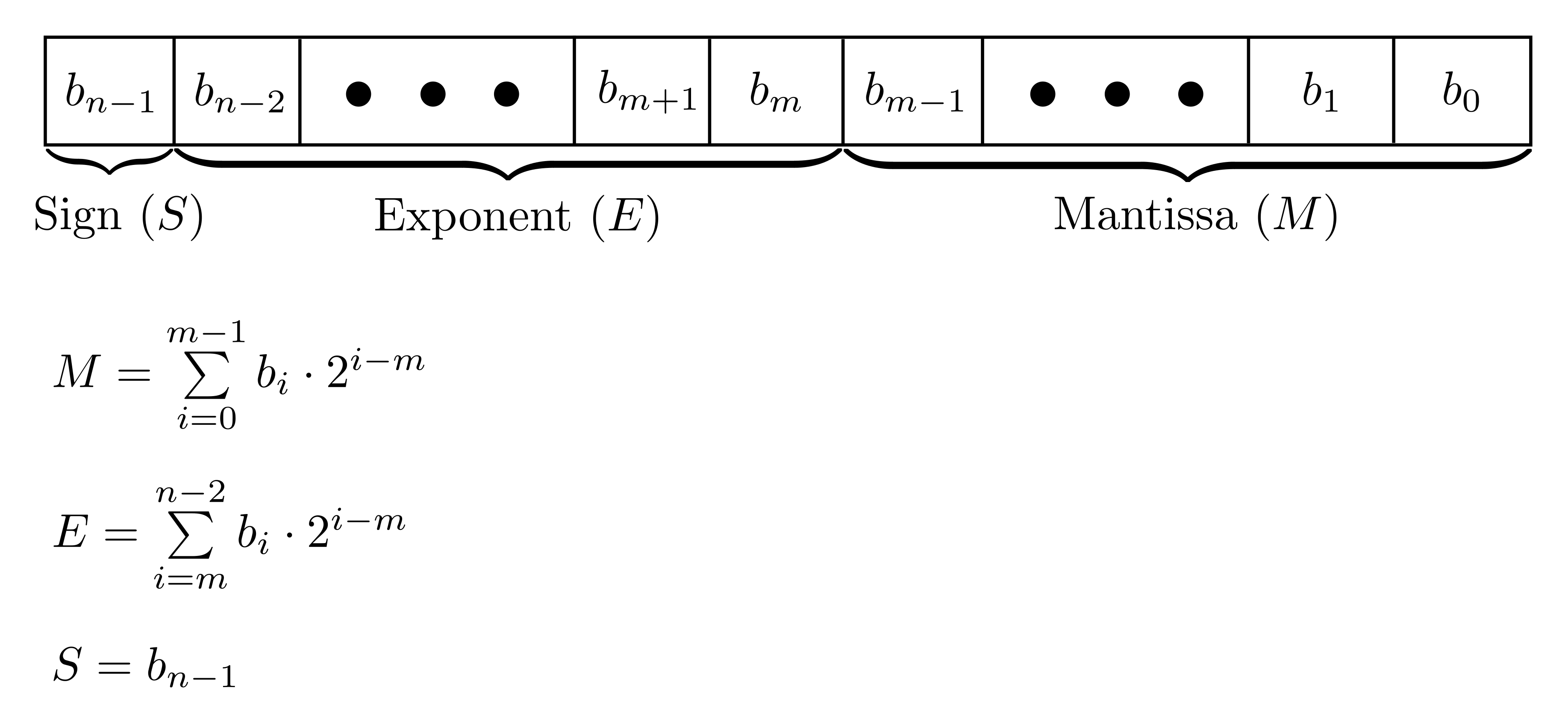
Figure 1: Binary representation of a floating-point number.

Floating-point types are characterized by the number of bits used for the exponent and for the mantissa. Increasing the exponent width extends the range of representable values, while increasing the mantissa width improves precision. Since all floating-point types include the sign bit, a shorthand notation typically specifies only the exponent and mantissa widths. For example, the E4M3 type is an 8-bit floating-point type with 4-bit exponent and 3-bit mantissa. Additionally, a floating-point type is specified by exponent bias - a number that is subtracted from the exponent during conversion from binary format to real value. Given the exponent width, mantissa width, and exponent bias, one can convert the binary representation of a floating-point type (except E8M0) into its real value using the following equation:

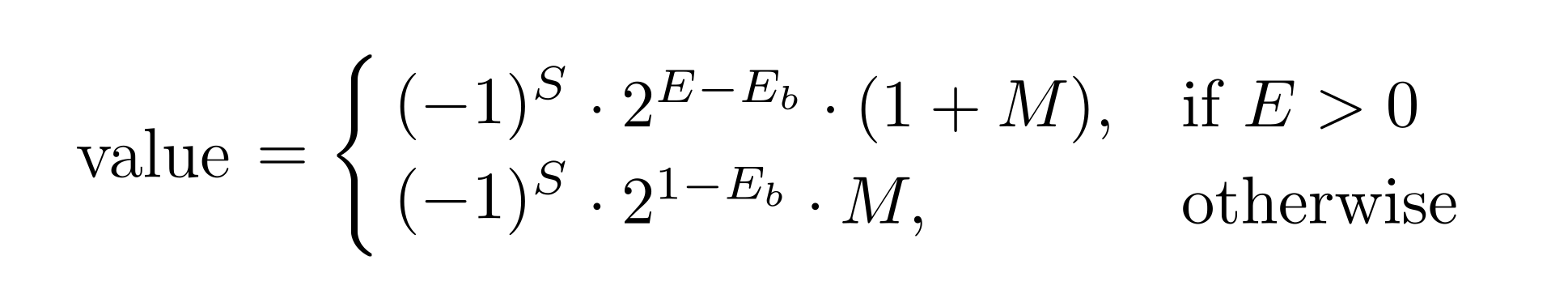
Figure 2: Conversion to real value from binary representation for floating-point numbers.

Please note that the equation takes different forms depending on whether the exponent is zero or not. Often, certain exponent and mantissa values are reserved for special values (e.g. NaN, Infinity), which limits the range of representable real numbers. For example, the FP16 type has 5-bit exponent with a nominal range of [0, 1, ... 2^5-1] = [0, 1, ... 31]. However, the exponent value E = 31 is reserved for NaN (if the mantissa M != 0) and infinity (if the mantissa M = 0). Therefore, the largest exponent value that can represent a real number is E = 30.

The following table summarizes low-precision types commonly used in modern AI/ML workloads:

Width	Shorthand	Exp. bias	Range	Zero	NaN	Infinity
16-Bit
	E5M10 (FP16)	15	±65504	S 00000 0000000000	S 11111 xxxxxxxxxx	S 11111 0000000000
	E8M7 (BF16)	127	±3.3895 * 10^38	S 00000000 0000000	S 11111111 xxxxxxx	S 11111111 0000000
8-Bit
	E4M3FN (FP8, OCP)	7	±448	S 0000 000	S 1111 111	n/a
	E4M3FNUZ (FP8)	8	±240	0 0000 000	1 0000 000	n/a
	E5M2 (BF8, OCP)	15	±57344	S 00000 00	S 11111 {01, 10 11}	S 11111 00
	E5M2FNUZ (BF8)	16	±57344	0 00000 00	S 00000 00	n/a
	E8M0	127	2^(±127)	n/a	11111111	n/a
6-Bit
	E2M3	1	±7.5	S 00 000	n/a	n/a
	E3M2 (BF6)	3	±28	S 000 00	n/a	n/a
4-Bit
	E2M1 (FP4)	1	±6	S 00 0	n/a	n/a

Please note that the E4M3 type has two variants: E4M3FN and E4M3FNUZ. Both E4M3FN and E4M3FNUZ use 4 bits for the exponent and 3 bits for the mantissa. They use different exponent biases and differ in the special values they can represent. Neither variant supports infinities, which is why their notations include FN (FiNite). However, E4M3FN supports +0, -0, +NaN and -Nan, while E4M3FNUZ supports only +0 and NaN, hence UZ (Unsigned Zero). The image below demonstrates how to convert a binary sequence into a real value, using E4M3FNUZ type as an example:

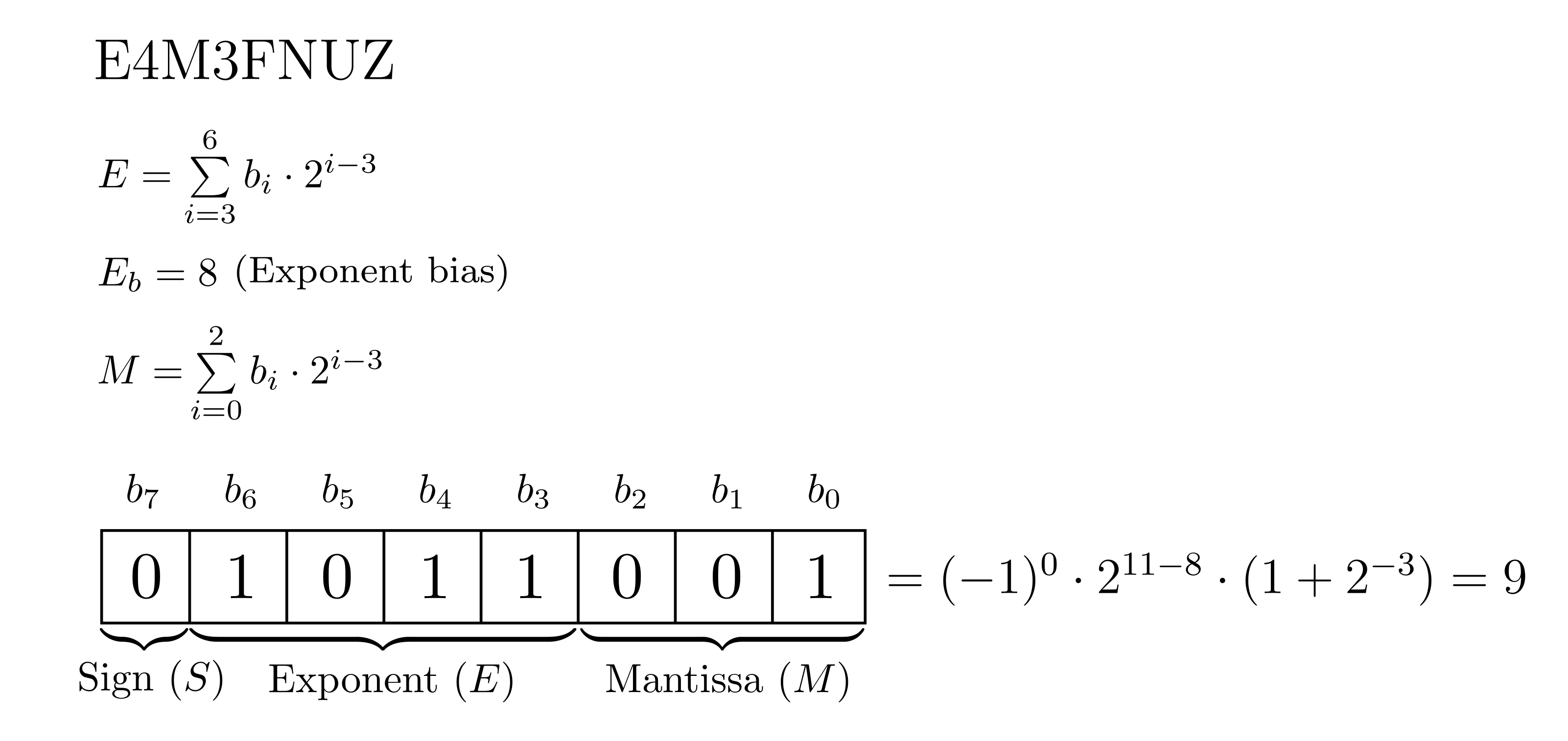
Figure 3: E4M3FNUZ encoding details.

FP8 types are divided into E4M3 and E5M2 formats. The E5M2 format is sometimes referred to as BF8, similar to BF16, where exponent width is larger compared to FP16. Similar to E4M3, E5M2 is further subdivided into two variants: E5M2 (OCP) and E5M2FNUZ. The AMD CDNA™3 architecture uses FNUZ variants for both E4M3 and E5M2, whereas the CDNA™4 architecture uses E4M3FN and E5M2 (OCP) variants. E4M3FN and E5M2 are standardized formats defined by the Open Compute Project (OCP). For detailed specifications, see the OCP Microscaling Formats (MX) Specification and the ONNX documentation. For visualization of FP8 values and their binary representations please refer to the FP8 Data table. Additionally, see the chapter “Low-precision floating-point types” in the AMD ROCm™ documentation for details on using low-precision types in HIP.

There is a special 8-bit format, E8M0, which is not used as a standard element data type but instead serves as a scale factor for microscaling types and block-scaled MFMA operations (discussed later in this article). Its value is calculated according to the equation below:

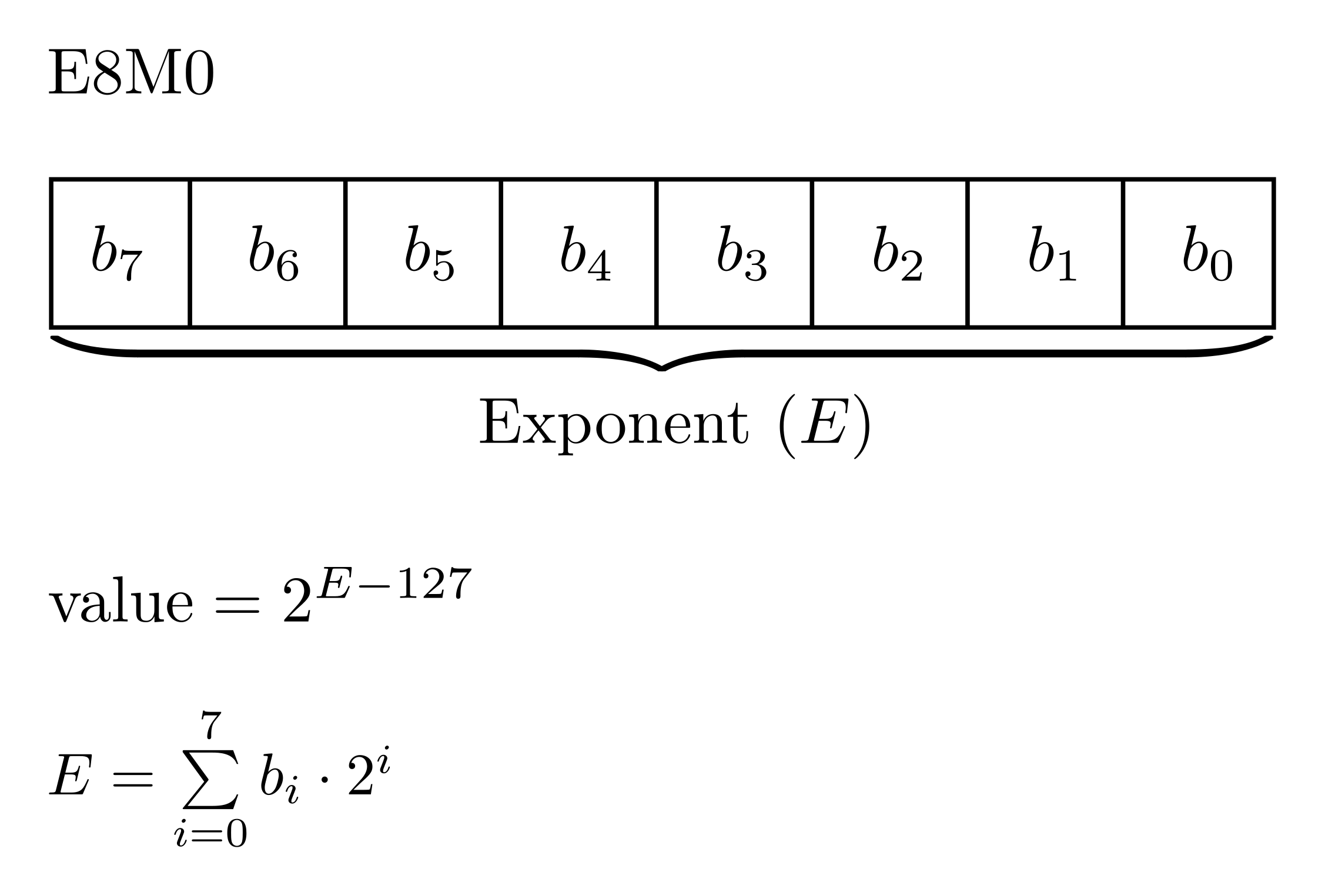
Figure 4: E8M0 encoding details.

The exponent value E = 255 is reserved for NaN values, limiting the range of representable real numbers to [2^-127 ... 2^127].

Similar to FP8, FP6 has two formats: E2M3 and E3M2. The latter, E3M2, is often referred to as BF6 due to its larger exponent width compared to E2M3.

Matrix fused-multiply-add (MFMA) Instructions#

The AMD CDNA™3 and CDNA™4 architectures support a variety of MFMA operations, which are characterized by the matrix dimensions M, N, K and the data type of input/output matrices. The following table lists all available floating-point MFMA instructions for the AMD CDNA™3 and CDNA™4 architectures. As can be seen from the table, the AMD CDNA™4 architecture extends the set of available MFMA instructions by adding new FP16/BF16 instructions with larger matrix dimensions. Furthermore, it introduces FP6/FP4 data types and provides a completely new set of FP8/FP6/FP4 instructions where the types can be independently used for the matrices A and B. Finally, the AMD CDNA™4 architecture enables MFMA with block exponent scaling.

Type (C,D) ← (A,B)	MxNxK (CDNA™3)	MxNxK (CDNA™4)	Cycles	Note
FP64 ← FP64	16x16x4	16x16x4	64
FP32 ← FP32	32x32x2	32x32x2	64
	16x16x4	16x16x4	32
FP32 ← FP16 (BF16)	32x32x8	32x32x8	32	Both A and B are either FP16 or BF16
	16x16x16	16x16x16	16
	-	16x16x32	16
	-	32x32x16	32
FP32 ← FP8	16x16x32	16x16x32	16	FP8 (E4M3) or BF8 (E5M2) can be used independently for A and B
	32x32x16	32x32x16	32
FP32 ← FP8/FP6/FP4	-	16x16x128	16 or 32	FP4, FP6 or FP8 can be used independently for A and B. Larger cycle count if either matrix A or B is FP8
	-	32x32x64	32 or 64
FP32 ← MXFP8/MXFP6/MXFP4	-	16x16x128	16 or 32	FP4, FP6 or FP8 can be used independently for A and B. Larger cycle count if either matrix A or B is FP8
	-	32x32x64	32 or 64

Please note that the table lists only floating-point type MFMA instructions with batch size = 1. In addition to them, the AMD CDNA™3 and CDNA™4 architectures support batched MFMA operations, where multiple output matrices are computed in parallel. These instructions are not covered in this article. See the Chapter 7 “Matrix Arithmetic Instructions” in the AMD CDNA™3 and AMD CDNA™4 ISA reference guides for the full list of available MFMA instructions.

The table above specifies cycle count for each MFMA operation. Given a known cycle count, one can estimate theoretical peak performance in TFLOP/s of corresponding MFMA operation using the formula below:

2*M*N*K * num_matrix_cores * (max_engine_clock / cycle_count) / 10^6,

where

num_matrix_cores is total number of matrix cores in a GPU (specified in white paper)
max_engine_clock is max engine clock (peak) in MHz (specified in white paper)
cycle_count is cycle count of corresponding MFMA instruction
M, N, K are matrix dimensions

Using this formula and the MFMA instruction 32x32x8 FP16 as an example, we can estimate theoretical peak FP16 Matrix Core performance on the AMD Instinct™ MI325X:

2*32*32*8 * 1216 * (2100 / 32) / 10^6 = 1307.4 TFLOP/s.

Compiler Intrinsics#

To use Matrix Core instructions in HIP kernels, LLVM provides built-in compiler intrinsic functions. The list of all available compiler intrinsics can be found in the LLVM Github repository. The syntax of the MFMA intrinsics has the following format:

d_reg = __builtin_amdgcn_mfma_ODType_MxNxKInDType(a_reg, b_reg, c_reg, cbsz, abid, blgp),

where

MxNxK specifies the shapes of the matrices A, B, C, D,
ODType is data type of the matrices C and D,
InDType is data type of the input matrices A and B,
a_reg is a scalar/vector containing a portion of the matrix A,
b_reg is a scalar/vector containing a portion of the matrix B,
c_reg is a vector containing a portion of the matrix C,
d_reg is a vector containing a portion of the matrix D,
cbsz, abid, blgp are broadcast flags. For the following discussion, these flags are irrelevant and are, therefore, set to 0 by default, unless specified otherwise. Please refer to the ISA reference guide for detailed information on the broadcast flags.

For example,

__builtin_amdgcn_mfma_f32_16x16x16f16 performs 16x16x16 MFMA, where both input matrices A and B have type FP16 and the output matrix has type FP32
__builtin_amdgcn_mfma_f32_32x32x16_fp8_fp8 performs 32x32x16 MFMA, where both input matrices A and B have type FP8(E4M3) and the output matrix is stored in FP32
__builtin_amdgcn_mfma_f32_32x32x16_fp8_bf8 performs 32x32x16 MFMA, where the matrix A has type FP8(E4M3) and the matrix B has type BF8(E5M2).

The MFMA instructions are wavefront-level (warp-level) instructions, where all work-items (threads) within a wavefront collectively perform a single MFMA operation and the operands A, B, C, D are distributed across work-items so that each work-item in the wavefront holds a portion of the operands. In order to use the MFMA instructions, it’s required to understand how the operands are distributed across threads within a wavefront. The ISA reference guide fully specifies the data layout for all available MFMA instructions. For illustrative purposes, the next chapter explains a subset of the MFMA instructions and the corresponding data layouts.

Examples#

Important note: In the following discussion we assume the matrices are stored in row-major order. The wavefront size on the AMD CDNA™ architecture is 64. The shapes of the matrices A, B, C, D are MxK, KxN, MxN, and MxN, respectively. The first dimension denotes the number of rows and the second dimension the number of columns in a matrix. For example, the matrix A has M rows and K columns.

__builtin_amdgcn_mfma_f32_32x32x2f32#

In this example we will multiply matrix A of size 32x2 with matrix B of size 2x32 using single wavefront (64 threads) and single MFMA instruction. The output matrix C has shape 32x32. The input and output matrices are FP32. Since threads within a wavefront collectively perform single MFMA instruction, the operands are distributed across the threads. Each thread stores

M * K / wavefront_size = 32 * 2 / 64 = 1 entries of the matrix A
K * N / wavefront_size = 2 * 32 / 64 = 1 entries of the matrix B
M * N / wavefront_size = 32 * 32 / 64 = 16 entries of the matrix C

The operands are distributed according to the scheme below. The matrix elements highlighted in light red are those stored by the thread with index 0 within the wavefront.

Figure 5: Data layout for `__builtin_amdgcn_mfma_f32_32x32x2f32`. The operands are stored in row-major order.

The code example below demonstrates how this operation can be implemented as a HIP kernel:

#include <hip/hip_runtime.h>

using fp32x16_t = __attribute__((vector_size(16 * sizeof(float)))) float;

__global__ void
mfma_fp32_32x32x2_fp32(const float* A, const float* B, float* C) {
    float a_reg;
    float b_reg;
    fp32x16_t c_reg {};

    const float* ldg_a_ptr = A + threadIdx.x / 32 + 2 * (threadIdx.x % 32);
    const float* ldg_b_ptr = B + threadIdx.x % 32 + (threadIdx.x / 32) * 32;

    a_reg = *ldg_a_ptr;
    b_reg = *ldg_b_ptr;

    c_reg = __builtin_amdgcn_mfma_f32_32x32x2f32(a_reg, b_reg, c_reg, 0, 0, 0);

    for (int i = 0; i < 4; i++) {
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + i * 32 * 8]          = c_reg[i * 4];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 1 + i * 32 * 8] = c_reg[i * 4 + 1];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 2 + i * 32 * 8] = c_reg[i * 4 + 2];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 3 + i * 32 * 8] = c_reg[i * 4 + 3];
    }
}

The GPU kernel can then be invoked on the host using a single wavefront:

mfma_fp32_32x32x2_fp32<<<1, 64>>>(A_device, B_device, C_device);

Please note that we use the vector data type fp32x16_t to store the entries of the matrix C in registers. Additionally, we zero-initialize c, since we compute C = A * B without accumulation.

__builtin_amdgcn_mfma_f32_16x16x16f16#

This example demonstrates how to multiply matrix A of size 16x16 with matrix B of size 16x16 using single wavefront (64 threads) and single MFMA instruction. The output matrix C has shape 16x16. The input matrices are stored in FP16 and the output matrix stored in FP32. In this case, each thread stores 4 entries of the matrix A, 4 entries of the matrix B and 4 entries of the matrix C. The data layout for this instruction is shown below. For illustrative purposes, the elements stored by the first thread within the wavefront are highlighted in red.

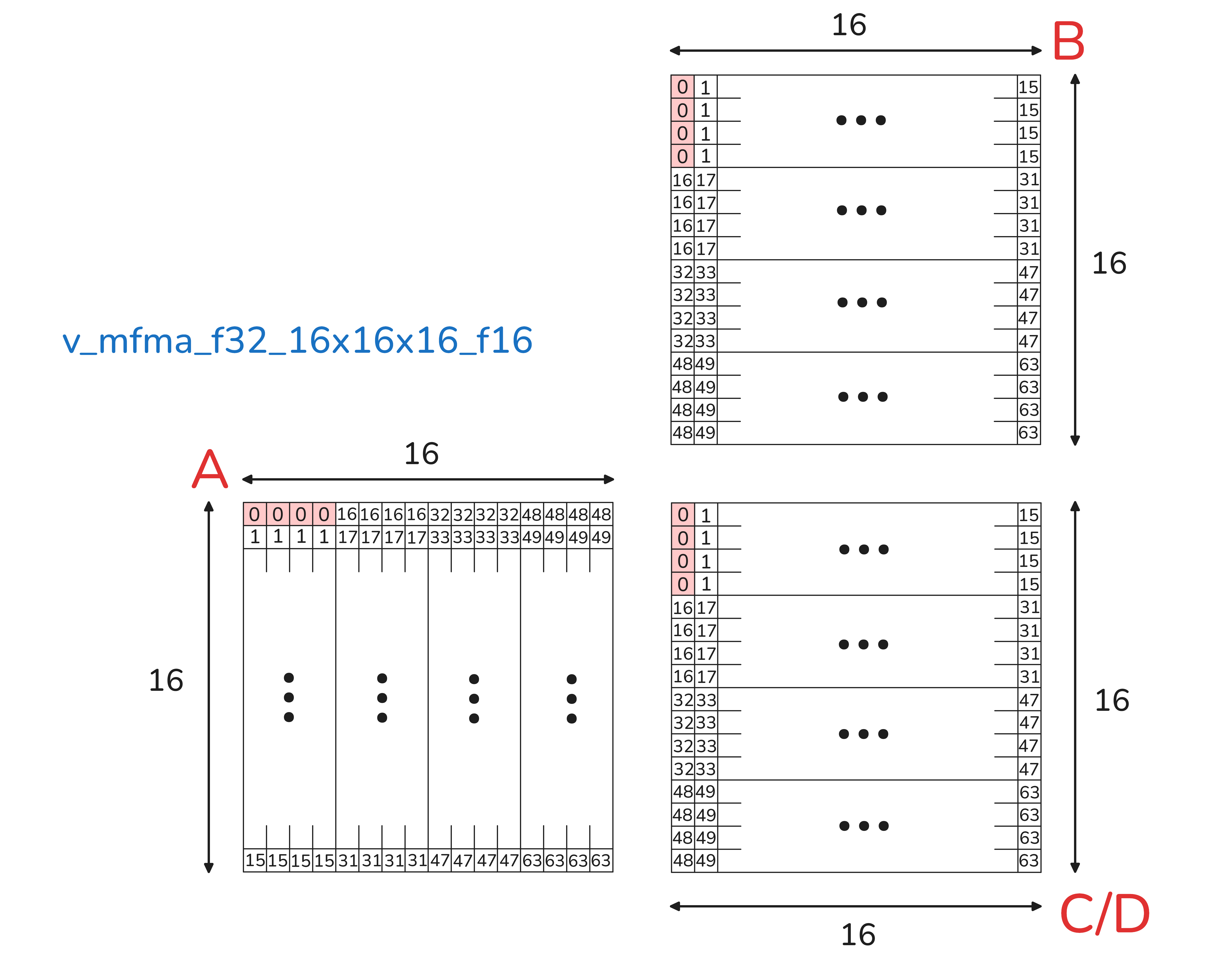
Figure 6: Data layout for __builtin_amdgcn_mfma_f32_16x16x16f16. The operands are stored in row-major order.

Corresponding HIP kernel is implemented below:

#include <hip/hip_runtime.h>
#include <hip/hip_fp16.h>

using fp16_t = _Float16;
using fp16x4_t = __attribute__((vector_size(4 * sizeof(fp16_t)))) fp16_t;
using fp32x4_t = __attribute__((vector_size(4 * sizeof(float)))) float;

__global__ void
mfma_fp32_16x16x16_fp16(const fp16_t* A, const fp16_t* B, float* C) {

    fp16x4_t a_reg;
    fp16x4_t b_reg;
    fp32x4_t c_reg {};

    a_reg = *reinterpret_cast<const fp16x4_t*>(A + 4 * (threadIdx.x / 16) + 16 * (threadIdx.x % 16));

    for (int i = 0; i < 4; i++) {
        b_reg[i] = *(B + i * 16 + threadIdx.x % 16 + (threadIdx.x / 16) * 64);
    }

    c_reg = __builtin_amdgcn_mfma_f32_16x16x16f16(a_reg, b_reg, c_reg, 0, 0, 0);

    for (int i = 0; i < 4; i++) {
        *(C + i * 16 + threadIdx.x % 16 + (threadIdx.x / 16) * 64) = c_reg[i];
    }
}

Please note that both __half and _Float16 types can be used in device code. However, the host supports only _Float16 type for arithmetic operations. As in the previous example, we use vector data types to store the matrix elements in registers.

__builtin_amdgcn_mfma_f32_32x32x16_fp8_fp8#

In this example we will multiply matrix A of size 32x16 with matrix B of size 16x32 using single wavefront (64 threads) and single MFMA instruction. The output matrix C has shape 32x32. The input matrices are stored in FP8 and the output matrix is stored in FP32. In this scenario, each thread stores 8 elements of the matrix A, 8 elements of the matrix B and 16 elements of the matrix C. The operands are distributed according to the scheme below. For illustrative purposes, the elements stored by the first thread within the wavefront are highlighted in red.

Figure 7: Data layout for __builtin_amdgcn_mfma_f32_32x32x16_fp8_fp8. The operands are stored in row-major order.

The code example below implements this operation as a HIP kernel:

#include <hip/hip_runtime.h>
#include <hip/hip_fp8.h>

using fp8_t = __hip_fp8_storage_t;
using fp8x8_t = __attribute__((vector_size(8 * sizeof(fp8_t)))) fp8_t;
using fp32x16_t = __attribute__((vector_size(16 * sizeof(float)))) float;

__global__ void
mfma_fp32_32x32x16_fp8_fp8(const fp8_t* A, const fp8_t* B, float* C) {
    fp8x8_t a_reg;
    fp8x8_t b_reg;
    fp32x16_t c_reg {};

    a_reg = *reinterpret_cast<const fp8x8_t*>(A + (threadIdx.x / 32) * 8 + (threadIdx.x % 32) * 16);

    for (int i = 0; i < 8; i++) {
        b_reg[i] = *(B + i * 32 + threadIdx.x % 32 + (threadIdx.x / 32) * 8 * 32);
    }

    c_reg = __builtin_amdgcn_mfma_f32_32x32x16_fp8_fp8((long)a_reg, (long)b_reg, c_reg, 0, 0, 0);

    for (int i = 0; i < 4; i++) {
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + i * 32 * 8]          = c_reg[i * 4];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 1 + i * 32 * 8] = c_reg[i * 4 + 1];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 2 + i * 32 * 8] = c_reg[i * 4 + 2];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 3 + i * 32 * 8] = c_reg[i * 4 + 3];
    }
}

To define FP8, we use __hip_fp8_storage_t type from hip_fp8.h. Note that the intrinsic function expects its first two operands to be of type long. To compile the code, the operands a and b are, therefore, converted to long.

__builtin_amdgcn_mfma_scale_f32_32x32x64_f8f8#

Important note: the MFMA instruction discussed in this example is supported only on AMD CDNA™4 GPUs (gfx950). Please make sure to install AMD ROCm™ version 7.0 or later.

The AMD CDNA™4 architecture introduces a new family of MFMA instructions with block exponent scaling. The syntax of these instructions differs from the classic MFMA compiler intrinsics:

d_reg = __builtin_amdgcn_mfma_scale_f32_MxNxK_f8f6f4(a_reg, b_reg, c_reg, Atype, Btype, OPSEL_A, scale_a, OPSEL_B, scale_b)

MxNxK specifies shapes of the matrices A, B, C, D
a_reg is a vector containing elements of the matrix A,
b_reg is a vector containing elements of the matrix B,
c_reg is a vector containing elements of the matrix C,
d_reg is a vector containing elements of the matrix D,
Atype is an integer that specifies the data type of the matrix A. The following values are possible: 0 = E4M3 (fp8), 1 = E5M2(bf8), 2 = E2M3(fp6), 3 = E3M2(bf6), 4 = E2M1(fp4),
Btype is an integer that specifies the data type of the matrix B. The following values are possible: 0 = E4M3 (fp8), 1 = E5M2(bf8), 2 = E2M3(fp6), 3 = E3M2(bf6), 4 = E2M1(fp4),
OPSEL_A, OPSEL_B are OPSEL codes. These arguments are not relevant for the discussion and therefore will be set to 0,
scale_a, scale_b are scalars / vectors containing scale factors of type E8M0.

As an example, let’s take a closer look at the instruction __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4. The inputs to this instruction are

Matrix A of size 32x64
Matrix Ax of size 32x2
Matrix B of size 64x32
Matrix Bx of size 2x32

The output matrix C has shape 32x32. Specifically, this instruction performs the following operation using single wavefront (64 threads):

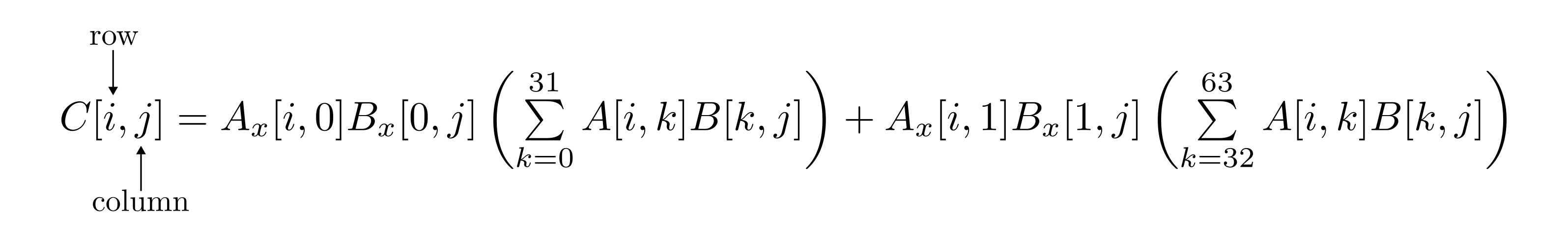
Figure 8: Block-scaled matrix multiplication via __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4.

During dot product operations, the scales Ax, Bx are applied after the normal dot product and prior to output/accumulation.

In this example, we will multiply two FP8 matrices using the __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4 intrinsic function. The input matrices A, B are stored in FP8 format, while the output matrix is stored in FP32. The scale matrices Ax, Bx contain elements of type E8M0. Each thread stores 32 entries from the matrix A, 1 entry from the matrix Ax, 32 entries from the matrix B, 1 entry from the matrix Bx and 16 entries from the matrix C. The operands are distributed according to the scheme below. Please note that this scheme is valid only if both input matrices A and B have FP8 type. For illustrative purposes, the matrix elements stored by the thread with threadIdx.x = 0 are highlighted in light red, while the elements stored by the thread with threadIdx.x = 32 within the wavefront are highlighted in light green.

Figure 9: Data layout for __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4 with FP8 input matrices. The operands are stored in row-major order.

The following code example shows how this operation can be implemented as a HIP kernel:

#include <hip/hip_runtime.h>
#include <hip/hip_ext_ocp.h>

using fp8_t = __amd_fp8_storage_t;
using fp8x32_t = __attribute__((vector_size(32 * sizeof(fp8_t)))) fp8_t;
using fp32x16_t = __attribute__((vector_size(16 * sizeof(float)))) float;

__global__ void
mfma_fp32_32x32x64_fp8_fp8(const fp8_t* A, const fp8_t* B, float* C) {
    fp8x32_t a_reg;
    fp8x32_t b_reg;
    fp32x16_t c_reg {};

    const fp8_t* ldg_a = A + (threadIdx.x % 32) * 64 + (threadIdx.x / 32) * 16;
    for (int i=0; i < 2; i++) {
        for (int j=0; j < 16; j++) {
            a_reg[i*16 + j] = *(ldg_a + i * 32 + j);
        }
    }

    const fp8_t* ldg_b = B + threadIdx.x % 32 + 32 * 16 * (threadIdx.x / 32);

    for (int i=0; i<2; i++) {
        for (int j=0; j < 16; j++) {
            b_reg[i*16 + j] = *(ldg_b + 32 * j + i * 32 * 32);
        }
    }

    uint8_t scale_a = 127;
    uint8_t scale_b = 127;

    c_reg = __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4(a_reg, b_reg, c_reg, 0, 0, 0, scale_a, 0, scale_b);

    for (int i = 0; i < 4; i++) {
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + i * 32 * 8]          = c_reg[i * 4];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 1 + i * 32 * 8] = c_reg[i * 4 + 1];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 2 + i * 32 * 8] = c_reg[i * 4 + 2];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 3 + i * 32 * 8] = c_reg[i * 4 + 3];
    }
}

Please note that in this example we use __amd_fp8_storage_t type defined in hip_ext_ocp.h to represent FP8. This library provides extensions APIs for low-precision and micro-scaling formats, and compared to hip_fp8.h, exposes a wider capability set. gfx950 provides hardware acceleration for these APIs. Most of the APIs are 1 to 1 mapping of hardware instruction. Additionally, we use uint8_t type to represent E8M0 scale factors. Since scale_a and scale_b encode exponent values, the corresponding actual scale factors are 2^(scale_a - 127) and 2^(scale_b - 127). If scale_a = scale_b = 127, the actual scale factors are equal to 1 and no scaling is applied.

__builtin_amdgcn_mfma_scale_f32_32x32x64_f4f4#

In our last example, we demonstrate how to multiply two FP4 matrices using the __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4 intrinsic function. As in the previous example, each thread stores 32 entries from the matrix A, 1 entry from the matrix Ax, 32 entries from the matrix B, 1 entry from the matrix Bx and 16 entries from the matrix C. The data layout for the output matrix remains the same as in the FP8 case. However, the data layout for the input matrices is different and depicted below. For illustrative purposes, the matrix elements stored by the thread with threadIdx.x = 0 are highlighted in light red, while the elements stored by the thread with threadIdx.x = 32 within the wavefront are highlighted in light green.

Figure 10: Data layout for __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4 with FP4 input matrices. The operands are stored in row-major order.

The code snippet below demonstrates how to implement this operation as a HIP kernel:

#include <hip/hip_runtime.h>
#include <hip/hip_ext_ocp.h>

using fp4x2_t = __amd_fp4x2_storage_t;
using fp4x64_t  = fp4x2_t __attribute__((ext_vector_type(32)));
using fp32x16_t = __attribute__((vector_size(16 * sizeof(float)))) float;

__global__ void
mfma_fp32_32x32x64_fp4_fp4(const fp4x2_t* A, const fp4x2_t* B, float* C) {

    fp4x64_t a_reg {};
    fp4x64_t b_reg {};
    fp32x16_t c_reg {};

    const fp4x2_t* ldg_a = A + (threadIdx.x % 32) * 32 + (threadIdx.x / 32) * 16;

    for (int i = 0; i < 16; i++) {
        a_reg[i] = *(ldg_a + i);
    }

    const fp4x2_t* ldg_b = B + (threadIdx.x % 32) / 2 + 16 * 32 * (threadIdx.x / 32);
    int b_extract_idx = threadIdx.x % 2;

    for (int i = 0; i < 16; i++) {
        uint8_t tmp0 = __amd_extract_fp4(*(ldg_b + 16 * 2 * i), b_extract_idx);
        uint8_t tmp1 = __amd_extract_fp4(*(ldg_b + 16 * (2 * i + 1)), b_extract_idx);
        b_reg[i] = __amd_create_fp4x2(tmp0, tmp1);
    }

    uint8_t scale_a = 127;
    uint8_t scale_b = 127;

    c_reg = __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4(a_reg, b_reg, c_reg, 4, 4, 0, scale_a, 0, scale_b);

    for (int i = 0; i < 4; i++) {
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + i * 32 * 8]          = c_reg[i * 4];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 1 + i * 32 * 8] = c_reg[i * 4 + 1];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 2 + i * 32 * 8] = c_reg[i * 4 + 2];
        C[threadIdx.x % 32 + (threadIdx.x / 32) * 4 * 32 + 32 * 3 + i * 32 * 8] = c_reg[i * 4 + 3];
    }
}

Since memory addressing is not allowed at a granularity smaller than 8 bits, we use __amd_fp4x2_storage_t (an alias for uint8_t) to store the input matrices and enable pointer operations. Note that the FP4 elements that need to be loaded from the matrix B are not contiguous in memory. To extract a single FP4 element, we use the __amd_extract_fp4 function provided in hip_ext_ocp.h. This function returns one FP4 element (of type uint8_t) from a fp4x2 vector, based on the index passed as the second argument:

uint8_t __amd_extract_fp4(const __amd_fp4x2_storage_t x, const size_t index) {
    if (index == 0) return (x & 0xFu);
    return (x >> 4);
}

Two FP4 values are then combined into __amd_fp4x2_storage_t using __amd_create_fp4x2:

__amd_fp4x2_storage_t __amd_create_fp4x2(const uint8_t x, const uint8_t y) {
    __amd_fp4x2_storage_t ret = 0;
    ret = x | (y << 4);
    return ret;
}

The compiler intrinsic function __builtin_amdgcn_mfma_scale_f32_32x32x64_f8f6f4 requires its first two arguments to be 256 bits wide. Since 32 FP4 elements occupy only 128 bits, we define fp4x64_t, which is 256 bits wide. In this type, 128 bits contain data, while the remaining 128 bits are zero. This allows us to pass a_reg and b_reg to the intrinsic function and compile the code successfully.

Summary#

In this article, we introduced Matrix Core instructions available on the AMD CDNA™3 and CDNA™4 architectures. We covered floating-point formats in detail, including modern low-precision element data types such as FP8, FP6, FP4, and the scale data type E8M0. We further explained how the floating-point types are represented as binary sequences and demonstrated, with concrete examples, how to convert their binary representations into real values. Next, we listed Matrix Core instructions supported by the modern CDNA™ architectures and discussed how to calculate the theoretical peak performance of Matrix Cores for specific MFMA instructions. To make the discussion more practical, we reviewed the compiler intrinsic functions that allow users to program Matrix Cores inside HIP kernels. Finally, we examined a subset of MFMA instructions in detail, providing code examples and illustrations to explain data layout and demonstrate how to implement simple mixed-precision MFMA operations in HIP. For additional information on Matrix Cores and low-precision data types, please refer to the following resources:

Disclaimers#

Third-party content is licensed to you directly by the third party that owns the content and is not licensed to you by AMD. ALL LINKED THIRD-PARTY CONTENT IS PROVIDED “AS IS” WITHOUT A WARRANTY OF ANY KIND. USE OF SUCH THIRD-PARTY CONTENT IS DONE AT YOUR SOLE DISCRETION AND UNDER NO CIRCUMSTANCES WILL AMD BE LIABLE TO YOU FOR ANY THIRD-PARTY CONTENT. YOU ASSUME ALL RISK AND ARE SOLELY RESPONSIBLE FOR ANY DAMAGES THAT MAY ARISE FROM YOUR USE OF THIRD-PARTY CONTENT.