Unlocking Sparse Acceleration on AMD GPUs with hipSPARSELt#

Sparse computation is a cornerstone of modern AI acceleration. As models like LLaMA and DINOv2 ViT-L scale in size and complexity, the demand for efficient matrix operations becomes increasingly critical. To address this, semi-structured sparsity, also known as the 2:4 structured sparsity pattern, has emerged as a powerful optimization technique.
AMD’s answer to this challenge is hipSPARSELt — a high-performance library designed to accelerate sparse matrix operations on AMD GPUs.
This blog explores:
What is structured sparsity (2:4 pattern)?
What is hipSPARSELt?
Performance comparisons between sparse and dense GEMM.
Structured Sparsity 2:4#
Structured sparsity refers to a regular pattern of zeroing out weights in a matrix. In the 2:4 sparsity pattern, every group of 4 consecutive weights contains exactly 2 zeros. This predictable structure enables hardware-friendly optimizations and efficient compression.
The Compression Ratio of the 2:4 Structured Sparsity Pattern#
A 2:4 sparse matrix consists of two components:
A compressed matrix, storing the two most important values from each group of four.
An index table, indicating the positions of the elements stored in the compressed matrix.
Figure 1 illustrates how a dense matrix is pruned and compressed into a structured 2:4 sparse matrix.
This process consists of two steps:
Step 1: Within each group of four consecutive elements along a row, select two elements to zero out such that the L1 norm of the remaining elements is maximized.
Step 2: Remove the zero elements and record the positions of the remaining non-zero elements (indices 0, 1, 2, or 3) in an index table.
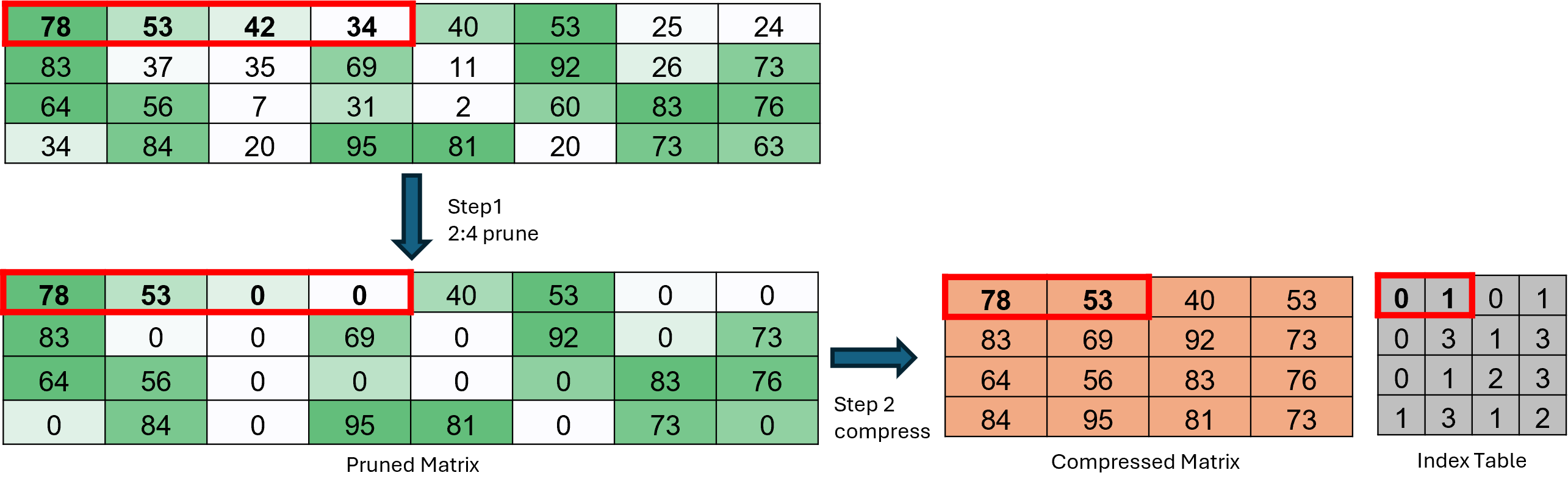 Figure 1. The steps for generating a 2:4 structured sparse matrix.
Figure 1. The steps for generating a 2:4 structured sparse matrix.
The compression ratio depends on the data type:
Float16 / BFloat16: 56.25%
Int8 / Float8: 62.5%
The formulas for calculating the compression ratio are:
What is hipSPARSELt?#
hipSPARSELt is a high-performance library developed by AMD for executing sparse matrix operations on GPUs. It is part of the ROCm (Radeon Open Compute) ecosystem and is implemented using the HIP (Heterogeneous-compute Interface for Portability) programming model.
Key Features#
Supports 2:4 structured sparsity matrix multiplication accelerated by AMD Matrix Core instructions.
Provides pruning and compression utilities to generate structured sparsity 2:4 matrices.
Supports operation fusion for activations (e.g., ReLU, GELU), scalar multipliers, and bias vectors.
Optimized for AMD discrete GPUs, starting from the MI300 series.
Figure 2 shows the workflow for performing sparse matrix multiplication using hipSPARSELt.
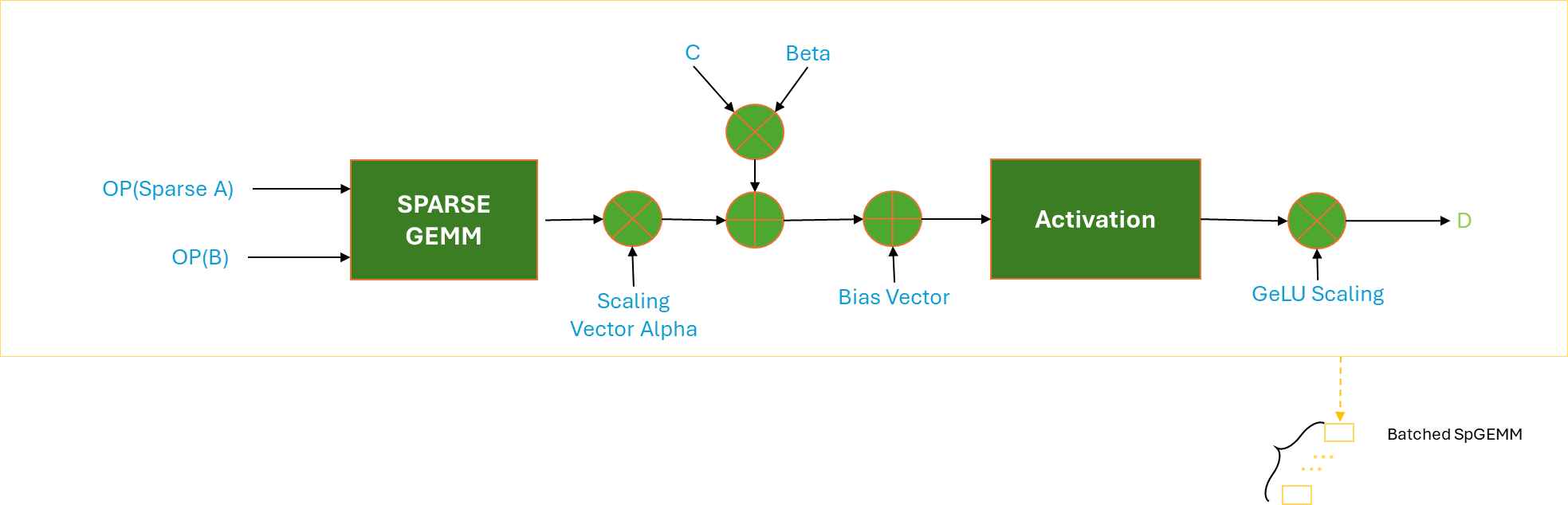 Figure 2. Operational overview of hipSPARSELt
Figure 2. Operational overview of hipSPARSELt
Sparse vs. Dense GEMM on AMD GPUs#
To evaluate the performance of hipSPARSELt, we benchmarked sparse and dense GEMM operations under the following setup:
Experimental Setup#
Dense GEMM: via hipBLASLt.
Sparse GEMM: via hipSPARSELt with 2:4 sparsity.
GPU: AMD MI300
Precision: FP16
Sparsity: 50% (2:4 enforced)
Matrix shapes are denoted as M × N × K, where:
Matrix A: M × K
Matrix B: K × N
Matrix C/D: M × N
“Op N” indicates non-transpose; “Op T” indicates transpose.
Performance Results#
Figures 3 and 4 present the relative speedup of sparse GEMM implemented with hipSPARSELt compared to dense GEMM implemented with hipBLASLt under different matrix configurations. Figure 3 shows the performance uplift when the K dimension is fixed, using an NN (non‑transpose × non‑transpose) layout with column‑major storage. Figure 4 reports the speedup when M = N is held constant, using a TN (transpose × non‑transpose) layout, also with column‑major storage.
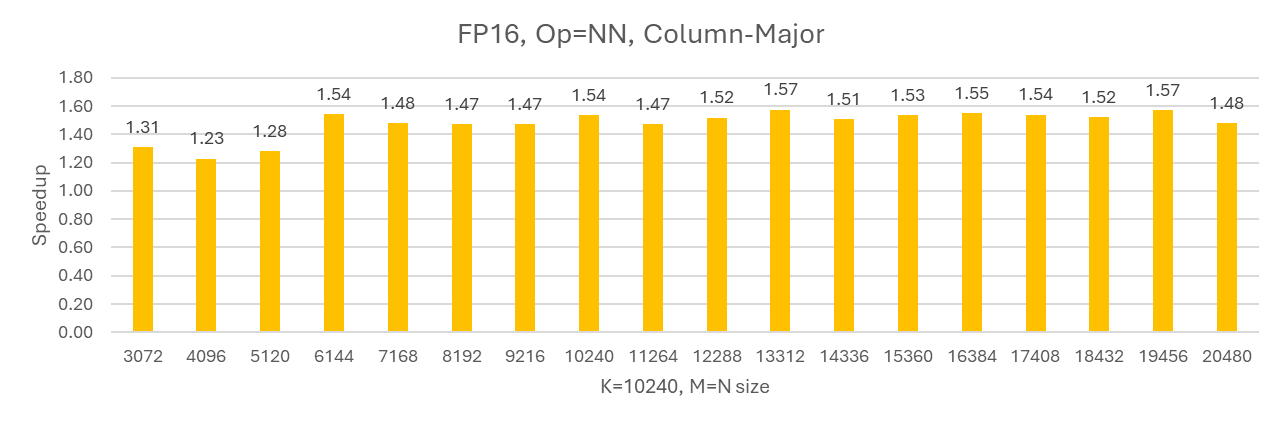 Figure 3. Speedup of Sparse GEMMs in hipSPARSELt over Dense GEMMs in hipBLASLt on AMD MI300 GPU , fp16 input/output, K fixed, NN layout, Column-major, ROCm 7.0
Figure 3. Speedup of Sparse GEMMs in hipSPARSELt over Dense GEMMs in hipBLASLt on AMD MI300 GPU , fp16 input/output, K fixed, NN layout, Column-major, ROCm 7.0
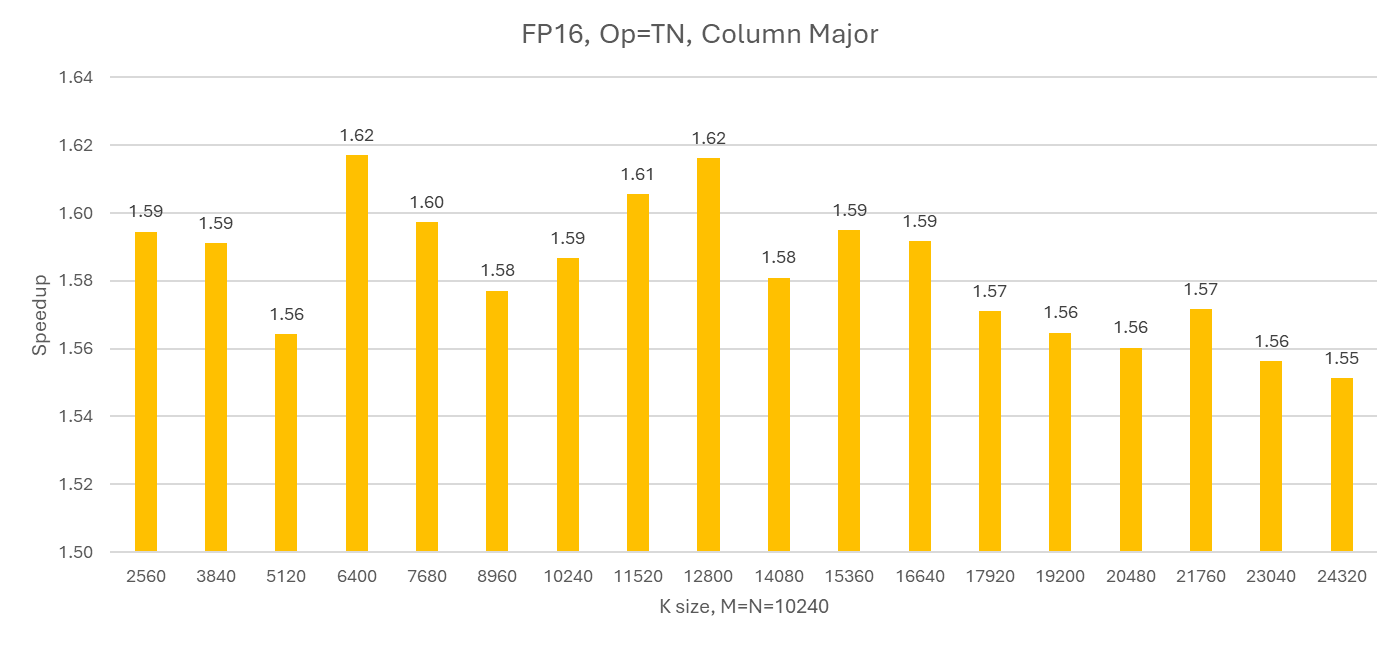 Figure 4. Speedup of Sparse GEMMs in hipSPARSELt over Dense GEMMs in hipBLASLt on AMD MI300 GPU , fp16 input/output, M=N fixed, TN layout, Column-major, ROCm 7.0
Figure 4. Speedup of Sparse GEMMs in hipSPARSELt over Dense GEMMs in hipBLASLt on AMD MI300 GPU , fp16 input/output, M=N fixed, TN layout, Column-major, ROCm 7.0
Code Example using hipSPARSELt#
The following example demonstrates how to use hipSPARSELt to perform sparse matrix multiplication on AMD GPUs.
This example includes:
Pruning matrix A and validating the result.
Compressing the pruned matrix.
Executing sparse matrix multiplication (SpMM). For more advanced code samples, please visit the hipSPARSELt Samples.
In this example, matrix A contains sequential values from 0 to 63, and it is multiplied by matrix B, which is filled entirely with ones. Please note that the memory layout is column-major.
#include <hip/hip_runtime.h>
#include <hipsparselt/hipsparselt.h>
#include <stdio.h>
void init_one(size_t m, size_t n, __half* in) {
for (size_t i = 0; i < m * n; i++) in[i] = static_cast<__half>(1);
}
void init_serial(size_t m, size_t n, __half* in) {
for (size_t i = 0; i < m * n; i++) in[i] = static_cast<__half>(i);
}
void print_matrix(size_t m, size_t n, __half* in) {
for (size_t i = 0; i < m; i++) {
for (size_t j = 0; j < n; j++) {
printf("%f\t", static_cast<float>(in[j * m + i]));
}
printf("\n");
}
}
int main() {
int64_t m = 8, n = 8, k = 8;
float alpha = 1.0f, beta = 0.0f;
hipsparseOperation_t trans_a = HIPSPARSE_OPERATION_NON_TRANSPOSE;
hipsparseOperation_t trans_b = HIPSPARSE_OPERATION_NON_TRANSPOSE;
hipsparseOrder_t order = HIPSPARSE_ORDER_COL;
int64_t row_a = m, col_a = k;
int64_t row_b = k, col_b = n;
int64_t row_c = m, col_c = n;
int64_t row_d = m, col_d = n;
// Host memory allocation
__half* hA = (__half*)malloc(row_a * col_a * sizeof(__half));
__half* hAp = (__half*)malloc(row_b * col_b * sizeof(__half));
__half* hB = (__half*)malloc(row_b * col_b * sizeof(__half));
__half* hC = (__half*)malloc(row_c * col_c * sizeof(__half));
__half* hD = (__half*)malloc(row_d * col_d * sizeof(__half));
// Initialize matrices A, B on host
init_serial(row_a, col_a, hA);
init_one(row_b, col_b, hB);
printf("A:\n");
print_matrix(row_a, col_a, hA);
// Device memory allocation
__half *dA, *dB, *dC, *dD;
hipMalloc(&dA, row_a * col_a * sizeof(__half));
hipMalloc(&dB, row_b * col_b * sizeof(__half));
hipMalloc(&dC, row_c * col_c * sizeof(__half));
hipMalloc(&dD, row_d * col_d * sizeof(__half));
// Copy data from host to device
hipMemcpy(dA, hA, row_a * col_a * sizeof(__half), hipMemcpyHostToDevice);
hipMemcpy(dB, hB, row_b * col_b * sizeof(__half), hipMemcpyHostToDevice);
hipMemcpy(dC, hC, row_c * col_c * sizeof(__half), hipMemcpyHostToDevice);
hipMemcpy(dD, hD, row_d * col_d * sizeof(__half), hipMemcpyHostToDevice);
// Initialize hipSPARSELt descriptors
hipsparseLtHandle_t handle;
hipsparseLtMatDescriptor_t matA, matB, matC, matD;
hipsparseLtMatmulDescriptor_t matmul;
hipsparseLtMatmulAlgSelection_t alg_sel;
hipsparseLtMatmulPlan_t plan;
hipStream_t stream = nullptr;
hipsparseLtInit(&handle);
hipsparseLtStructuredDescriptorInit(&handle, &matA, row_a, col_a, row_a, 16, HIP_R_16F, order,
HIPSPARSELT_SPARSITY_50_PERCENT);
hipsparseLtDenseDescriptorInit(&handle, &matB, row_b, col_b, row_b, 16, HIP_R_16F, order);
hipsparseLtDenseDescriptorInit(&handle, &matC, row_c, col_c, row_c, 16, HIP_R_16F, order);
hipsparseLtDenseDescriptorInit(&handle, &matD, row_d, col_d, row_d, 16, HIP_R_16F, order);
hipsparseLtMatmulDescriptorInit(&handle, &matmul, trans_a, trans_b, &matA, &matB, &matC, &matD,
HIPSPARSELT_COMPUTE_32F);
hipsparseLtMatmulAlgSelectionInit(&handle, &alg_sel, &matmul, HIPSPARSELT_MATMUL_ALG_DEFAULT);
hipsparseLtMatmulPlanInit(&handle, &plan, &matmul, &alg_sel);
// Prune matrix A
__half* dP;
hipMalloc(&dP, row_a * col_a * sizeof(__half));
hipsparseLtSpMMAPrune(&handle, &matmul, dA, dP, HIPSPARSELT_PRUNE_SPMMA_STRIP, stream);
// Check pruning validity
int* d_valid;
hipMalloc(&d_valid, sizeof(int));
hipsparseLtSpMMAPruneCheck(&handle, &matmul, dP, d_valid, stream);
int is_valid;
hipMemcpyAsync(&is_valid, d_valid, sizeof(int), hipMemcpyDeviceToHost, stream);
hipStreamSynchronize(stream);
if (is_valid != 0) {
std::cerr << "Matrix A was not pruned correctly." << std::endl;
return EXIT_FAILURE;
}
hipStreamSynchronize(stream);
// Copy pruned back to host
hipMemcpy(hAp, dP, row_a * col_a * sizeof(__half), hipMemcpyDeviceToHost);
printf("Pruned A:\n");
print_matrix(row_a, col_a, hAp);
// Compress pruned matrix A
size_t compressed_size, compress_buffer_size;
hipsparseLtSpMMACompressedSize(&handle, &plan, &compressed_size, &compress_buffer_size);
void *d_compressed, *d_compressBuffer;
hipMalloc(&d_compressed, compressed_size);
hipMalloc(&d_compressBuffer, compress_buffer_size);
hipsparseLtSpMMACompress(&handle, &plan, dP, d_compressed, d_compressBuffer, stream);
// Allocate workspace
size_t workspace_size;
hipsparseLtMatmulGetWorkspace(&handle, &plan, &workspace_size);
void* d_workspace;
hipMalloc(&d_workspace, workspace_size);
// Perform sparse matrix multiplication
int num_streams = 1;
hipStream_t streams[1] = {stream};
hipsparseLtMatmul(&handle, &plan, &alpha, d_compressed, dB, &beta, dC, dD, d_workspace, streams,
num_streams);
hipStreamSynchronize(stream);
// Copy result back to host
hipMemcpy(hD, dD, row_d * col_d * sizeof(__half), hipMemcpyDeviceToHost);
printf("Result:\n");
print_matrix(row_d, col_d, hD);
// Cleanup
hipsparseLtMatDescriptorDestroy(&matA);
hipsparseLtMatDescriptorDestroy(&matB);
hipsparseLtMatDescriptorDestroy(&matC);
hipsparseLtMatDescriptorDestroy(&matD);
hipsparseLtMatmulPlanDestroy(&plan);
hipsparseLtDestroy(&handle);
hipFree(dA); hipFree(dB); hipFree(dC); hipFree(dD); hipFree(dP);
hipFree(d_compressed); hipFree(d_compressBuffer); hipFree(d_workspace);
free(hA); free(hB); free(hC); free(hD); free(hAp);
}
Here’s the CMake configuration file used to build the sample above.
add_executable(sample_spmm sample_spmm.cpp)
find_package(hip REQUIRED CONFIG PATHS /opt/rocm)
set(CMAKE_CXX_COMPILER /opt/rocm/llvm/bin/clang++)
target_link_libraries(sample_spmm PRIVATE hipsparselt)
set_target_properties(sample_spmm PROPERTIES
CXX_STANDARD 17
CXX_STANDARD_REQUIRED ON
CXX_EXTENSIONS OFF
RUNTIME_OUTPUT_DIRECTORY "${PROJECT_BINARY_DIR}"
)
target_include_directories(sample_spmm
SYSTEM PRIVATE
$<BUILD_INTERFACE:${HIP_INCLUDE_DIRS}>
)
target_compile_options(sample_spmm PRIVATE -mf16c)
target_compile_definitions(sample_spmm PRIVATE ROCM_USE_FLOAT16)
target_link_libraries(sample_spmm PRIVATE hip::host hip::device)
Place the CMakeLists.txt file and the sample_spmm.cpp source file in the same directory, then run cmake . && make to generate the executable.
Summary#
In this blog, we explored how hipSPARSELt empowers AMD GPUs to efficiently execute sparse matrix operations using the 2:4 structured sparsity pattern. This semi-structured format enables predictable compression and acceleration, reducing memory usage and improving inference speed.
With support for fusion operations, pruning utilities, and AMD Matrix Core acceleration, hipSPARSELt is a powerful tool for deploying sparse AI models like Sparse LLaMA. Benchmarks on AMD MI300 GPUs show significant speedups over dense GEMM (about 1.3x~), making hipSPARSELt a key enabler for high-performance, efficient deep learning workloads.
Disclaimers#
Third-party content is licensed to you directly by the third party that owns the content and is not licensed to you by AMD. ALL LINKED THIRD-PARTY CONTENT IS PROVIDED “AS IS” WITHOUT A WARRANTY OF ANY KIND. USE OF SUCH THIRD-PARTY CONTENT IS DONE AT YOUR SOLE DISCRETION AND UNDER NO CIRCUMSTANCES WILL AMD BE LIABLE TO YOU FOR ANY THIRD-PARTY CONTENT. YOU ASSUME ALL RISK AND ARE SOLELY RESPONSIBLE FOR ANY DAMAGES THAT MAY ARISE FROM YOUR USE OF THIRD-PARTY CONTENT.