Slim Down Your Llama: Pruning & Fine-Tuning for Maximum Performance#

In this blog, we demonstrate how quantization, intelligent depth pruning and supervised fine-tuning can dramatically improve the inference performance of Meta’s Llama 3.1 405B model on AMD Instinct MI355X GPUs. By applying quantization and reducing the number of layers from the original 126, we are able to decrease memory requirements and boost token throughput. Additionally, with carefully applied fine-tuning, we maintain high inference accuracy for both RougeL and Exact Match metrics on MLPerf workloads. To see how these optimizations fit into AMD’s broader MLPerf Inference v5.1 efforts, read Reproducing the AMD Instinct™ GPUs MLPerf Inference v5.1 Submission. For a detailed technical breakdown into other optimizations, check out our Technical Dive into AMD’s MLPerf Inference v5.1 Submission.
Quantizing Llama 3.1 405B with MXFP4#
Llama 3.1 405B is one of the most advanced open-source large language models. In its original BF16 format, the model is 756 GB. Thanks to the MI355X’s support for MXFP4 quantization, we can quantize the model to approximately 207 GB. With its 288 GB HBM capacity, the MI355X can efficiently host the entire MXFP4 version of Llama 3.1 405B on a single GPU, eliminating the need for model sharding across multiple devices.
Intelligent Model Pruning#
Our intelligent model pruning approach offers two strategies: (1) conservative pruning, dropping fewer layers (e.g., 26 out of 126) to maintain accuracy with minimal impact, as shown in Table 3, and (2) aggressive pruning, dropping more layers (e.g., 42 out of 126) followed by fine-tuning to recover accuracy, as shown in Table 4.
The Llama 3.1 405B model comprises 126 architecturally identical layers. However, not all layers contribute equally to token generation. Using a calibration dataset, we calculate the importance of each transformer layer by measuring the sum of the output magnitudes before the final RMSNorm layer, defined as \(L_i = \sum(|output_i|)\), where \(L_i\) is the importance score of the \(i^{th}\) layer, and \(output_i\) is the output tensor of the transformer layer’s feed-forward network (FFN) before RMSNorm.
Using 170 samples from the calibration dataset, we identify and drop contiguous layers with lower importance scores to minimize accuracy loss. The chart below (Figure 1) illustrates the layer importance scores for the FP4 model of Llama 3.1 405B, calculated based on the output magnitude at the end of each of its 126 layers, using a calibration dataset of 170 samples. The x-axis represents the layer index, while the y-axis shows the normalized output magnitude. The chart reveals significant variation in layer importance scores across the 126 layers, with layers closer to the maximum layer index exhibiting the highest scores. In our experiments, we will primarily focus on dropping layers within the highlighted region (layer indices 56 to 107) to minimize the impact of depth-pruning on model accuracy.
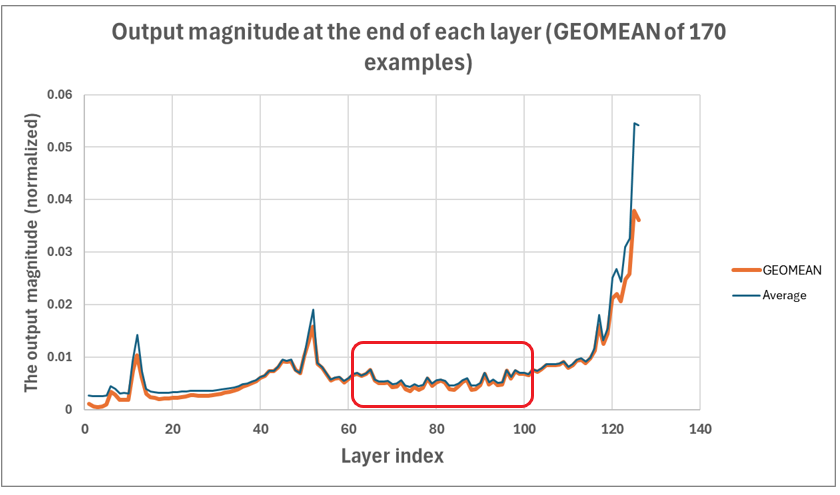
Figure 1: Layer importance scores for 126 layers of the FP4-quantized Llama 3.1 405B model.#
Table 1 compares performance across different pruning strategies, each dropping 42 layers. The first column indicates the number of dropped layers and their index range. Despite dropping the same number of layers, performance varies significantly, with generated tokens/s ranging from 2,307 to 2,921 and Exact Match accuracy from 78.35% to 88.78%. For subsequent experiments, we choose to drop layers 62 to 103, followed by supervised fine-tuning to optimize Exact Match accuracy.
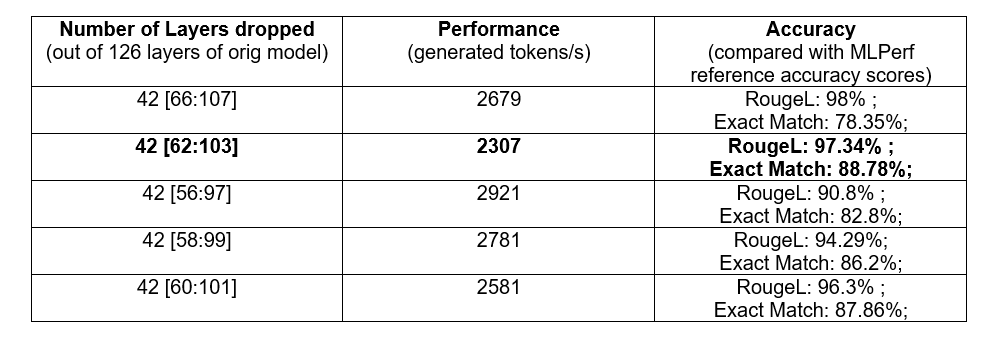
Table 1: Performance comparison of different depth-pruning strategies with 42 dropped layers.#
Model Fine Tuning#
Pruning the FP4 model of Llama 3.1 405B inevitably reduces its accuracy. To mitigate this, we employ Supervised Fine-Tuning (SFT) to restore the accuracy of the pruned model. Our approach involves pruning the original BF16 version of Llama 3.1 405B by removing the same layers as in the FP4 model, then training a LoRA adapter on the pruned BF16 model. Subsequently, we integrate the trained BF16 LoRA adapter with the pruned BF16 model and quantize the result to FP4. This process yields our final fine-tuned and pruned FP4 Llama 3.1 405B model, optimized for inference.
According to MLPerf guidelines, the Llama 3.1 405B model must meet accuracy criteria for both RougeL and Exact Match metrics in MLPerf workloads. Table 2 reveals that Exact Match accuracy experiences more significant degradation than RougeL accuracy after layer pruning. To enhance Exact Match accuracy, we generate “needle in a haystack” (NIAH) multivalue datasets and apply LoRA (Low-Rank Adaptation) fine-tuning to train a LoRA adapter on the pruned BF16 Llama 3.1 405B model, improving overall accuracy. Table 2 details the impact of pruning different numbers of layers in the FP4 Llama 3.1 405B model, with the first column specifying the number of dropped layers and their corresponding index range.

Table 2: Accuracy and performance with varying numbers of dropped layers for the FP4-quantized Llama 3.1 405B model.#
Training an effective LoRA adapter involves several key steps. First, it is essential to prepare both training and validation datasets tailored for the NIAH multivalue datasets, aiming to improve the Exact Match accuracy of the pruned model. In our experiments, we selected needle values of 8, 16, and 32 bytes, along with sequence lengths of 8k, 12k, and 16k tokens for the generated samples. This approach ensures comprehensive coverage of the Llama 3.1 405B MLPerf workloads, where input sequence lengths range from 476 to 19,988 tokens, with an average of 9,428 tokens.
Next, proper configuration of the LoRA parameters is crucial. In our experiments, we used r=16 and lora_alpha=16. Finally, ensuring the correct system prompt formats during LoRA fine-tuning is vital to achieve the expected accuracy of the fine-tuned model. Below is an example of the lora_config values used in our experiments:
lora_config = LoraConfig(
r=16,
lora_alpha=16,
target_modules=["q_proj", "k_proj", "v_proj", "o_proj", "down_proj", "gate_proj", "up_proj"],
lora_dropout=0.05,
bias="none",
task_type=TaskType.CAUSAL_LM
)
We explored three options for the final fine-tuned and pruned model:
Pruned FP4 model + fine-tuned FP4 LoRA adapter.
Pruned FP4 model + fine-tuned BF16 LoRA adapter.
Combined pruned BF16 model with fine-tuned BF16 LoRA adapter, quantized to FP4.
For options 1 and 2, we explored running separate inference paths for the pruned FP4 Llama 3.1 405B model and the fine-tuned FP4/BF16 LoRA adapter, then combining their results. However, this approach introduces performance overhead, reducing the rate of generated tokens per second due to the dual inference paths. Consequently, we adopted option 3 for our experiments to mitigate this issue.
For options 1 and 2, the combination of inference results from the pruned FP4 Llama 3.1 405B model and the fine-tuned FP4/BF16 LoRA adapter is expressed as:
where, \(x\) is the input sequence, \(f(x)\) represents the inference output of the pruned FP4 base model, \(loraAdapt(x)\) is the inference output of the fine-tuned LoRA adapter, \(r\) is the rank value used in LoRA fine-tuning, and \(\alpha\) is a fixed hyperparameter controlling the influence of the fine-tuned low-rank matrices.
For option 3, we combine the model weights of the fine-tuned BF16 LoRA adapter with the pruned FP16 Llama 3.1 405B model using the equation:
where, \(W'\) is the final weight matrix after LoRA fine-tuning, \(W_0\) is the pre-trained weight matrix, \(\delta{W}\) represents the weight update, \(r\) is the rank value in LoRA fine-tuning, \(\alpha\) is a fixed hyperparameter regulating the influence of the low-rank matrices, and \(B\) and \(A\) are the low-rank matrices employed in LoRA fine-tuning, \(q_n\) is the quantization noise introduced during the FP4 quantization process.
Performance and Accuracy Results#
Table 3 shows that pruning 26 layers (~21%) from the original 126-layer Llama 3.1 405B model increases token throughput significantly compared to the baseline FP4 model, while maintaining high accuracy: above 96% for Exact Match and above 99.6% for RougeL metrics. This demonstrates that selective layer pruning maintains high accuracy.

Table 3: Performance and accuracy with intelligent model pruning.#
Table 4 shows that pruning 42 layers (33.3%) combined with LoRA fine-tuning yields a significant increase in token throughput compared to the baseline FP4 model, with Exact Match accuracy above 96.7% and RougeL accuracy above 97.7%. Without fine-tuning, Exact Match accuracy drops to 88.8%, highlighting the critical role of supervised fine-tuning in recovering accuracy after aggressive pruning.

Table 4: Performance and accuracy with and without fine-tuning for pruned model.#
Summary#
This blog presents two strategies for optimizing the Llama 3.1 405B model: (1) conservative pruning, removing fewer layers (e.g., 26) to maintain high accuracy, as shown in Table 3; and (2) aggressive pruning, removing more layers (e.g., 42) followed by LoRA fine-tuning to restore accuracy, as shown in Table 4.
Our end-to-end solution combines quantization, intelligent pruning, and fine-tuning to achieve significant performance gains while maintaining high accuracy (above 97% for RougeL and 96% for Exact Match) per MLPerf evaluation rules. This approach enables efficient deployment of large models like Llama 3.1 405B on AMD Instinct MI355X GPUs. For a broader view of AMD’s MLPerf Inference v5.1 submissions, see Reproducing the AMD Instinct™ GPUs MLPerf Inference v5.1 Submission. For a deeper technical exploration, visit our Technical Dive into AMD’s MLPerf Inference v5.1 Submission.
Disclaimers#
Third-party content is licensed to you directly by the third party that owns the content and is not licensed to you by AMD. ALL LINKED THIRD-PARTY CONTENT IS PROVIDED “AS IS” WITHOUT A WARRANTY OF ANY KIND. USE OF SUCH THIRD-PARTY CONTENT IS DONE AT YOUR SOLE DISCRETION AND UNDER NO CIRCUMSTANCES WILL AMD BE LIABLE TO YOU FOR ANY THIRD-PARTY CONTENT. YOU ASSUME ALL RISK AND ARE SOLELY RESPONSIBLE FOR ANY DAMAGES THAT MAY ARISE FROM YOUR USE OF THIRD-PARTY CONTENT.